| Re: [eigen] Google Summer of Code 2018 - Symmetric Matrices for Eigen |
[ Thread Index | Date Index | More lists.tuxfamily.org/eigen Archives ]
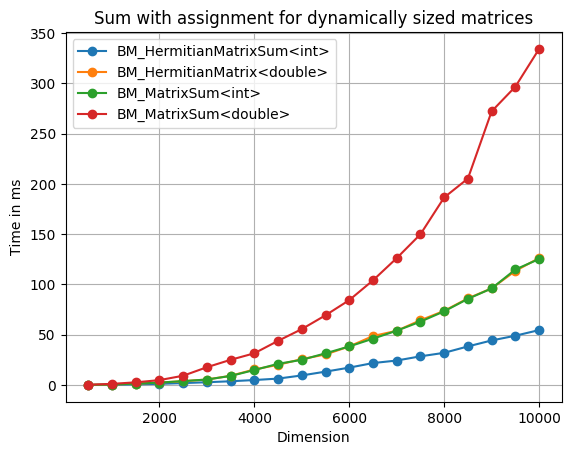
Hello together, first of all: Thank you again for supporting the idea of implementing a class for hermitian matrices in Eigen. I would be happy if you could give me some feedback on what I have implemented so far: I've decided to name the class HermitianMatrix and to store either the upper or lower triangular part in rectangular full packed format as suggested by some of you. For further information about this storage format see The current implementation consists of the following functionality: 1. Constructors to build a HermitianMatrix by passing a dense Matrix. The elements are stored in a dense Matrix in either row or column major. 2. Core evaluators for providing the methods coeff(), coeffRef() and the operator () 3. Sum and difference assignment operators += and -= 4. CwiseBinaryOp for supporting addition and subtraction of two hermitian matrices. 5. Assignment of CwiseBinaryOp to HermitianMatrix. All methods try to use transform the problems of hermitian matrices to problems of the underlying dense matrix that stores the matrix elements. A problem I'm currently facing is the following: In the case of complex scalars, I want to support real hermitian and not just symmetric matrices. That means when the upper triangular part of a matrix is stored in RFPF and the method coeff() or coeffRef() is called for an element in the lower triangular part, the complex conjugated should be returned. Any idea how this could be handled? I have benchmarked (using Google benchmark) some functionality I've implemented and it looks very good. As an attachment you find some of the benchmark results for addition (including evaluation) for fixed and dynamically sized matrices. I would be really happy about some feedback. All the best, David |
Running ./sum_with_assignment_dynamic Run on (8 X 2300 MHz CPU s) CPU Caches: L1 Data 32K (x4) L1 Instruction 32K (x4) L2 Unified 262K (x4) L3 Unified 6291K (x1) -------------------------------------------------------------------------- Benchmark Time CPU Iterations -------------------------------------------------------------------------- BM_HermitianMatrixSum<int>/500 40842 ns 40839 ns 16874 BM_HermitianMatrixSum<int>/1000 179075 ns 179055 ns 3931 BM_HermitianMatrixSum<int>/1500 545291 ns 545134 ns 1194 BM_HermitianMatrixSum<int>/2000 1117085 ns 1117051 ns 627 BM_HermitianMatrixSum<int>/2500 1854680 ns 1854175 ns 366 BM_HermitianMatrixSum<int>/3000 2719936 ns 2719722 ns 263 BM_HermitianMatrixSum<int>/3500 3675831 ns 3675587 ns 189 BM_HermitianMatrixSum<int>/4000 4905195 ns 4904090 ns 134 BM_HermitianMatrixSum<int>/4500 6331792 ns 6329981 ns 104 BM_HermitianMatrixSum<int>/5000 9469737 ns 9468338 ns 71 BM_HermitianMatrixSum<int>/5500 13265203 ns 13264098 ns 51 BM_HermitianMatrixSum<int>/6000 17246663 ns 17246675 ns 40 BM_HermitianMatrixSum<int>/6500 21793114 ns 21791061 ns 33 BM_HermitianMatrixSum<int>/7000 24307023 ns 24307034 ns 29 BM_HermitianMatrixSum<int>/7500 28498900 ns 28487320 ns 25 BM_HermitianMatrixSum<int>/8000 31986509 ns 31984591 ns 22 BM_HermitianMatrixSum<int>/8500 38354968 ns 38337294 ns 17 BM_HermitianMatrixSum<int>/9000 44294826 ns 44292933 ns 15 BM_HermitianMatrixSum<int>/9500 49010163 ns 49010000 ns 13 BM_HermitianMatrixSum<int>/10000 54598965 ns 54596250 ns 12 BM_HermitianMatrixSum<double>/500 79776 ns 79774 ns 8279 BM_HermitianMatrixSum<double>/1000 460592 ns 460568 ns 1385 BM_HermitianMatrixSum<double>/1500 1271036 ns 1271035 ns 508 BM_HermitianMatrixSum<double>/2000 2376715 ns 2376549 ns 295 BM_HermitianMatrixSum<double>/2500 3753730 ns 3752721 ns 183 BM_HermitianMatrixSum<double>/3000 5409910 ns 5409910 ns 111 BM_HermitianMatrixSum<double>/3500 9117958 ns 9116368 ns 76 BM_HermitianMatrixSum<double>/4000 15416583 ns 15411319 ns 47 BM_HermitianMatrixSum<double>/4500 20023412 ns 20012061 ns 33 BM_HermitianMatrixSum<double>/5000 25765077 ns 25761148 ns 27 BM_HermitianMatrixSum<double>/5500 30329416 ns 30327652 ns 23 BM_HermitianMatrixSum<double>/6000 38334114 ns 38333059 ns 17 BM_HermitianMatrixSum<double>/6500 48696232 ns 48688000 ns 14 BM_HermitianMatrixSum<double>/7000 53890019 ns 53889000 ns 12 BM_HermitianMatrixSum<double>/7500 64413929 ns 64394444 ns 9 BM_HermitianMatrixSum<double>/8000 73745602 ns 73744667 ns 9 BM_HermitianMatrixSum<double>/8500 86173302 ns 86162286 ns 7 BM_HermitianMatrixSum<double>/9000 96114298 ns 96106000 ns 7 BM_HermitianMatrixSum<double>/9500 113459816 ns 113453800 ns 5 BM_HermitianMatrixSum<double>/10000 126311952 ns 126305400 ns 5 BM_MatrixSum<int>/500 82016 ns 82015 ns 7838 BM_MatrixSum<int>/1000 458210 ns 458207 ns 1366 BM_MatrixSum<int>/1500 1314947 ns 1314784 ns 551 BM_MatrixSum<int>/2000 2364923 ns 2363754 ns 297 BM_MatrixSum<int>/2500 3815049 ns 3814777 ns 184 BM_MatrixSum<int>/3000 5404607 ns 5404604 ns 111 BM_MatrixSum<int>/3500 8981025 ns 8980865 ns 74 BM_MatrixSum<int>/4000 14844169 ns 14843021 ns 48 BM_MatrixSum<int>/4500 21050318 ns 21045406 ns 32 BM_MatrixSum<int>/5000 24990336 ns 24990320 ns 25 BM_MatrixSum<int>/5500 31500755 ns 31496773 ns 22 BM_MatrixSum<int>/6000 38326938 ns 38305235 ns 17 BM_MatrixSum<int>/6500 46071499 ns 46071538 ns 13 BM_MatrixSum<int>/7000 53987554 ns 53983667 ns 12 BM_MatrixSum<int>/7500 63014770 ns 63002700 ns 10 BM_MatrixSum<int>/8000 73295392 ns 73290556 ns 9 BM_MatrixSum<int>/8500 85687893 ns 85685143 ns 7 BM_MatrixSum<int>/9000 96045342 ns 96041286 ns 7 BM_MatrixSum<int>/9500 114898166 ns 114824333 ns 6 BM_MatrixSum<int>/10000 125300289 ns 125299400 ns 5 BM_MatrixSum<double>/500 178109 ns 178091 ns 3733 BM_MatrixSum<double>/1000 1093186 ns 1093153 ns 593 BM_MatrixSum<double>/1500 2612725 ns 2612725 ns 265 BM_MatrixSum<double>/2000 4814101 ns 4814109 ns 129 BM_MatrixSum<double>/2500 9187167 ns 9187178 ns 73 BM_MatrixSum<double>/3000 17640873 ns 17636333 ns 39 BM_MatrixSum<double>/3500 25020597 ns 25018074 ns 27 BM_MatrixSum<double>/4000 31511644 ns 31511000 ns 21 BM_MatrixSum<double>/4500 43899589 ns 43899133 ns 15 BM_MatrixSum<double>/5000 55585714 ns 55583727 ns 11 BM_MatrixSum<double>/5500 69329502 ns 69324778 ns 9 BM_MatrixSum<double>/6000 84413952 ns 84414286 ns 7 BM_MatrixSum<double>/6500 104098243 ns 104085667 ns 6 BM_MatrixSum<double>/7000 126201333 ns 126198400 ns 5 BM_MatrixSum<double>/7500 149953446 ns 149947750 ns 4 BM_MatrixSum<double>/8000 186563867 ns 186515667 ns 3 BM_MatrixSum<double>/8500 205372371 ns 205367667 ns 3 BM_MatrixSum<double>/9000 272266877 ns 272238500 ns 2 BM_MatrixSum<double>/9500 296817304 ns 296818000 ns 2 BM_MatrixSum<double>/10000 334373061 ns 334344000 ns 2
2018-06-10 22:56:02 Running ./sum_with_assignment_fixed Run on (8 X 2300 MHz CPU s) CPU Caches: L1 Data 32K (x4) L1 Instruction 32K (x4) L2 Unified 262K (x4) L3 Unified 6291K (x1) ------------------------------------------------------------------------- Benchmark Time CPU Iterations ------------------------------------------------------------------------- BM_HermitianMatrixSum<int, 5> 2 ns 2 ns 298234029 BM_HermitianMatrixSum<int, 10> 5 ns 5 ns 130853351 BM_HermitianMatrixSum<int, 15> 9 ns 9 ns 72996507 BM_HermitianMatrixSum<int, 20> 24 ns 24 ns 28478090 BM_HermitianMatrixSum<int, 25> 37 ns 37 ns 18147691 BM_HermitianMatrixSum<int, 30> 52 ns 52 ns 12703022 BM_HermitianMatrixSum<int, 35> 75 ns 75 ns 8540543 BM_HermitianMatrixSum<int, 40> 96 ns 96 ns 6990563 BM_HermitianMatrixSum<int, 45> 250 ns 250 ns 2800538 BM_HermitianMatrixSum<int, 50> 145 ns 145 ns 4604627 BM_HermitianMatrixSum<int, 55> 537 ns 537 ns 1244157 BM_HermitianMatrixSum<int, 60> 210 ns 210 ns 3347905 BM_HermitianMatrixSum<int, 65> 246 ns 246 ns 2831543 BM_HermitianMatrixSum<int, 70> 286 ns 285 ns 2476596 BM_HermitianMatrixSum<int, 75> 371 ns 370 ns 1962918 BM_HermitianMatrixSum<int, 80> 549 ns 549 ns 1227618 BM_HermitianMatrixSum<int, 85> 732 ns 732 ns 933308 BM_HermitianMatrixSum<int, 90> 787 ns 786 ns 857192 BM_HermitianMatrixSum<int, 95> 868 ns 868 ns 733414 BM_HermitianMatrixSum<int, 100> 985 ns 985 ns 672198 BM_MatrixSum<int, 5> 2 ns 2 ns 309601631 BM_MatrixSum<int, 10> 8 ns 8 ns 89557586 BM_MatrixSum<int, 15> 26 ns 26 ns 26726840 BM_MatrixSum<int, 20> 45 ns 45 ns 16098319 BM_MatrixSum<int, 25> 82 ns 82 ns 8534816 BM_MatrixSum<int, 30> 115 ns 114 ns 6036825 BM_MatrixSum<int, 35> 155 ns 155 ns 4354290 BM_MatrixSum<int, 40> 575 ns 575 ns 1207417 BM_MatrixSum<int, 45> 245 ns 245 ns 2829026 BM_MatrixSum<int, 50> 299 ns 299 ns 2386895 BM_MatrixSum<int, 55> 541 ns 540 ns 1249242 BM_MatrixSum<int, 60> 1321 ns 1320 ns 471501 BM_MatrixSum<int, 65> 956 ns 956 ns 646735 BM_MatrixSum<int, 70> 947 ns 947 ns 668769 BM_MatrixSum<int, 75> 1201 ns 1201 ns 556001 BM_MatrixSum<int, 80> 1238 ns 1237 ns 528877 BM_MatrixSum<int, 85> 1751 ns 1751 ns 404704 BM_MatrixSum<int, 90> 1685 ns 1683 ns 431130 BM_MatrixSum<int, 95> 1785 ns 1785 ns 366951 BM_MatrixSum<int, 100> 1882 ns 1882 ns 360970 BM_HermitianMatrixSum<double, 5> 3 ns 3 ns 248628989 BM_HermitianMatrixSum<double, 10> 13 ns 13 ns 54507795 BM_HermitianMatrixSum<double, 15> 27 ns 27 ns 24455259 BM_HermitianMatrixSum<double, 20> 47 ns 47 ns 14704647 BM_HermitianMatrixSum<double, 25> 79 ns 79 ns 8203542 BM_HermitianMatrixSum<double, 30> 109 ns 109 ns 6031155 BM_HermitianMatrixSum<double, 35> 434 ns 434 ns 1584625 BM_HermitianMatrixSum<double, 40> 560 ns 559 ns 1197871 BM_HermitianMatrixSum<double, 45> 486 ns 485 ns 1444195 BM_HermitianMatrixSum<double, 50> 290 ns 290 ns 2329660 BM_HermitianMatrixSum<double, 55> 1143 ns 1143 ns 555036 BM_HermitianMatrixSum<double, 60> 1241 ns 1241 ns 523752 BM_HermitianMatrixSum<double, 65> 843 ns 843 ns 805449 BM_HermitianMatrixSum<double, 70> 970 ns 970 ns 676904 BM_HermitianMatrixSum<double, 75> 1138 ns 1137 ns 601406 BM_HermitianMatrixSum<double, 80> 1161 ns 1161 ns 541498 BM_HermitianMatrixSum<double, 85> 1440 ns 1440 ns 476778 BM_HermitianMatrixSum<double, 90> 1570 ns 1570 ns 417803 BM_HermitianMatrixSum<double, 95> 1696 ns 1696 ns 392377 BM_HermitianMatrixSum<double, 100> 1941 ns 1941 ns 354538 BM_MatrixSum<double, 5> 4 ns 4 ns 171998201 BM_MatrixSum<double, 10> 15 ns 15 ns 44088934 BM_MatrixSum<double, 15> 50 ns 50 ns 13798541 BM_MatrixSum<double, 20> 275 ns 275 ns 2462690 BM_MatrixSum<double, 25> 147 ns 147 ns 4651997 BM_MatrixSum<double, 30> 612 ns 612 ns 1114898 BM_MatrixSum<double, 35> 278 ns 278 ns 2513835 BM_MatrixSum<double, 40> 535 ns 534 ns 1164415 BM_MatrixSum<double, 45> 784 ns 784 ns 840891 BM_MatrixSum<double, 50> 1764 ns 1764 ns 370412 BM_MatrixSum<double, 55> 1158 ns 1158 ns 545460 BM_MatrixSum<double, 60> 1575 ns 1574 ns 420085 BM_MatrixSum<double, 65> 1670 ns 1670 ns 405266 BM_MatrixSum<double, 70> 1891 ns 1891 ns 349376 BM_MatrixSum<double, 75> 2137 ns 2137 ns 321496 BM_MatrixSum<double, 80> 2467 ns 2467 ns 283429 BM_MatrixSum<double, 85> 3777 ns 3773 ns 186393 BM_MatrixSum<double, 90> 3179 ns 3178 ns 220694 BM_MatrixSum<double, 95> 3445 ns 3445 ns 199336 BM_MatrixSum<double, 100> 4542 ns 4542 ns 153002
|
| Mail converted by MHonArc 2.6.19+ | http://listengine.tuxfamily.org/ |